 其它
其它
趋势网讯:你花时间写微博、交朋友、挖八卦,还用剩下的时间来亲自建立友谊。但悲哀的是,尽管做了这么多努力,你的朋友可能还是比你大多数朋友少。但不要绝望,我们大多数人都是这样。一般来说我们的朋友比我们受欢迎。
不相信?想想最近Johan Ugander、Brian Karrer、Lars Backstrom 、Cameron Marlow最近写的有关Facebook的论文吧。(信息披露:Ugander是康奈尔的学生,我是他博士论文答辩委员会成员。)他们调查了Facebook上所有的活跃用户(当时为7.21亿人,约为世界人口的10%),其中共有690亿对好友关系。研究人员研究了用户们的数量与其朋友的朋友数量,发现93%的用户的朋友数量低于他朋友的朋友数量的平均值。之后,他们从整体上对Facebook进行了研究,发现平均一个用户有190个朋友,而他们的朋友平均有635个朋友。
对线下社交网络的研究也发现了同样的趋势。这与每个人的性格无关,只是一个基本的算数问题。一个人朋友的朋友平均数量总是大于这个人朋友的数量。只要社交网络有人朋友多有人朋友少,这条定理就必然存在。
这一现象被称之为好友悖论,其根本原因是一种在很多其他情况下都会出现数学模型(一种特别的“加权平均数“模型”)。了解了这种模型能帮你化解一些生活中的小烦恼。
比如说你现在走进了一家健身房。看看周围,是不是觉得好像每个人的身材都比你好?恩,你也许是对的,但这种情况无法避免而且完全不需要因此觉得惭愧。如果你只是一个普通的健身房会员,根据预期你就应该看到这样的场景,因为那些大汗淋漓喘着粗气的人不代表平均值。他们是那种会花时间在健身房的类型,所以你才会第一眼就看到他们。那些沙发土豆正窝在家里你没法把他们算在内。换句话说,你所取的健身馆会员这个样本不具有代表性,它其中健身迷的比例偏多。
这也解释了为何人们总觉得机场、餐馆、公园、海滩的拥挤程度总大于实际统计的平均值。这些地方没人的时候,没有人在场见证它们的空空如也。
加权平均数是用在这些情况下自然会用到的方法。这里有个例子来说明全球教育界如何说明自己的运行状况。比如一个教授教两个班,一个是面向90名新生的基础课程,另一个是有十个高年级学生的高级研习班。这个教授平均一个班有多少人?
学校大概会说50个人,因为 (90 + 10)/2 = 50。教授也会同意这种算法。这种算法默认两个班是一样的,一般平均数都是这么算的:把总数的一半分到90个人的班,再把另一半分到10个人的班,得到的数量正好在两者的中间。这种算法没错,不过在这种情况下有些误导性。
想要了解其中的原因,就从学生的角度来思考一下这个问题。大多数学生(100个学生中有90人)发现自己坐在有90人的大班级里,只要十个人体验过10个人的课堂。当然这必然会让学生眼里的平均数更接近90而不是10,因此也会高于50。
为了计算学生眼里的平均数,假设我们在每个班让每个人进行投票。如果你问他们“你们班有多少人?”,90个学生会回答“90”还有10个会回答“10”。他们答案的总数为:(90x90)+(10x10)=8200。
由于总共有90 + 10 = 100名学生,他们感觉平均班级的大小等于8,200/100=82,这比学校广告里说的平均50人的班级要大很多。
我希望你们注意这一模式(请把这一模式刻在神经里,我们之后还需要用到它们)。在这一模式里,90和10各自扮演了两个角色。正因如此在计算学生眼里的平均数的算式里出现了两个90两个10。
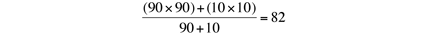
![]() 马斯克女儿爆料
马斯克女儿爆料 ![]() 吃娃娃菜中毒夫妻最高判刑十年以上
吃娃娃菜中毒夫妻最高判刑十年以上 ![]() 男子1650元买羽绒服全是飞丝报警
男子1650元买羽绒服全是飞丝报警
每个数字用两次这一模型将是我们理解好友悖论的关键所在。
下面详细讲解一个小例子,这样最能说明社交网络中的这个模式了。(我所说的任何内容都不依赖特定网络结构。只要网络中每个人朋友的数量有多有少,这一结果都会出现。我挑这个小网络只是想算起来容易一点。)
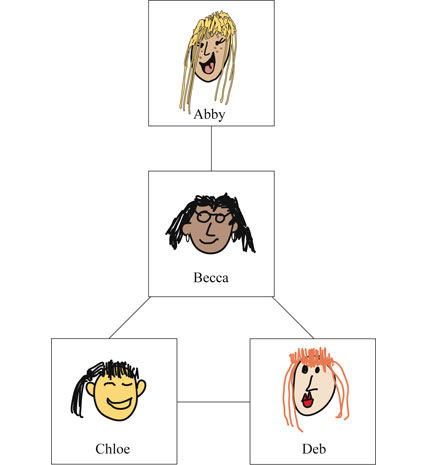
在这个案例中,Abby, Becca, Chloe和Deb是四个高中生,连线代表连互为好友。如果两个人都视对方为好友,她们之间就会连起来。
Becca是Abby唯一的好友,她是个小交际花,和每个人都是朋友。Chole和Deb是朋友,她们也是Becca的朋友。因此Abby有一个朋友,Becca有三个,Chole和Deb各有两个,加起来共有8个朋友。由于共有4个人,平均每个人有2个朋友。
2这个平均数代表好友悖论里平均每个人的朋友数量。记住,好友悖论声称这个数量比平均朋友的朋友数量小,但真实如此吗?这个问题有点让人头昏是因为这句话念起来比较拗口。不停的说或者写或者想“朋友的朋友”很容易感到恶心。为了避免这种情况,我们用朋友的“分数”来表示朋友的朋友的数量。所有问题就成了:“你的圈子里所有朋友的平均分是多少?”
假设每个女孩都会喊出她的朋友的分数,一名记录员会等在一旁记录下这些分数的平均值。
Abby:“Becca得了三分。”
Becca:“Abby一分,Chloe两分,Deb两分。”
Chloe:“Becca三分,Deb两分。”
Deb: “Becca三分,Chloe两分。”
把这些分数加起来3 + 1 + 2 + 2 + 3 + 2 + 3 + 2,等于18。由于一共有八个分数,因此平均值是18除以8,等于2.25。
注意2.25比2大。看来朋友平均分分数的确比女孩自己的高。正因如此好友悖论的理论才会是真的。
关键在于这一现象为什么会发生。这是因为Becca这样受欢迎的人不仅分数高,被朋友提到的次数也多,因此对平均分的贡献不成比例的高。看看Becca是怎么样把平均数变成18的吧:Abby被提到了一次,因为她的得分是1(只被一个朋友提到),因此她对总分的贡献是1x1;Becca被提到了三次因为她的分数是3,因此她的贡献是3X3;Chloe和Deb都被提到了两次,每次贡献两分,因此为总分贡献了2x2。所以这四个人的总分是(1 x 1) + (3 x 3) + (2 x 2) + (2 x 2),而相应的平均分是:
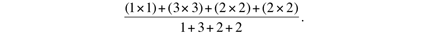
这是1,3,2,2这四个数的加权平均分,这种每个数用两次的模式在班级规模的问题中也一样存在。看看上面的算式你就明白了。每个人的得分乘以自己了一次然后才相加。这个平方的做法令大数字所占的比重更多重(就像上面的例子中Becca的3分一样),平均分也因此提高了。
正因如此,我们会直观感觉自己朋友的朋友比自己的朋友多。朋友的分数是平方后的加权平均数,因此总是比没有以这种方式加权的自己的分数高。
一旦发现了这种结构,其他定律的证明也就变成了普通的数学问题(见问后说明)。
与很多美好的数学思想一样,好友悖论也有很多令人振奋的实际应用,这些是其发现者未曾预见的。最近根据好友悖论建立了一个早期报警系统以预防流行病爆发。
哈佛大学一项在2009年H1N1禽流感期间进行了一项研究,科学家Nicholas Christakis和James Fowler随机监测了一大群本科生以及他们提到的一小群朋友(这也是这项研究聪明的地方)感染流感的状况。很明显,他们的朋友就和哨兵一样——他们比普通大学生早两个星期生病,这大概是因为他们总体上与其他人联系更紧密。这和好友悖论预期的一样。这两周时间对公共健康部门官员及早采取措施以预防大面积感染非常重要。
这一点不容小视。